摘  要  炉顶布料制度是高炉最重要的制度，而布料溜槽的形式对布料存在关键性影响，目前溜槽形式有横截面半圆形溜槽和方形，本文通过对两种溜槽的进行了对比，通过matlab软件模拟计算找出了不同溜槽的布料特点，为溜槽的使用和角度选择提供了依据。

关键词  高炉  溜槽  matlab

1  概述

邯钢炼铁部五高炉有效容积为2000m3高炉，2005年由1260m3高炉改造而成，采用全皮带上料，炉顶并罐式料罐。并罐布料偏析是由于炉料进入料罐后流动产生粒级偏析，布料过程中料流在溜槽上偏析布引起，主要表现在炉料在料面上的落点轨迹和圆周方向的料流流量[1]，并罐形式炉顶布料由于料罐中心线与产生较大偏析，由于并列料罐的布置，炉料从料流阀流出后下落到中心喉管，在中心喉管偏行，这样在溜槽一圈的旋转中，炉料落到溜槽上的速度和落点都不同，这就导致炉料在料面上的质量分布不均匀[2]，但由于布料过程中产生一定的布料偏析，特别是由于半圆形圆周摩擦力较小，导致炉料布料落点范围较宽，休风后发现整个溜槽中部出现炉料摩擦的痕迹，说明整个布料过程炉料已经出现脱离溜槽布料控制的情况，高炉后期通过对矿批和焦批的调整后取得了一定的效果，但矿批和焦批有一定的局限性。后设计使用方溜槽，方形溜槽由于边缘直角形，边缘力较大，可以将炉料很好控制，落点较集中，但由于前期没有使用过方溜槽，布料角度和矿批等都需要从新衡量，因此对两种溜槽进行了模型计算。

2  布料溜槽模拟计算

2.1圆形溜槽布料情况

圆形布料溜槽示意图及相关受力分析见图1。

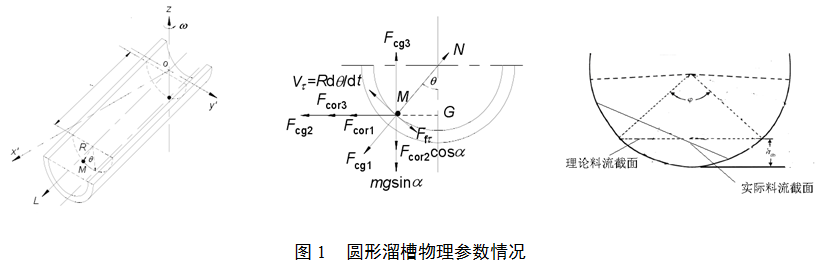
2.1.1  圆形溜槽布料数值设定

由于炉料落点主要受离开溜槽时的速度影响，因此对溜槽尾端炉料速度进行分解研究，可将炉料离开溜槽后速度分为x，y，z三个方向上的抛物自由落体运动，其中的vx，、vy、vz；设定料线为H，Q为炉料流量kg/s，S为料流开口面积m2，ρ为密度kg/m3，高炉布料溜槽转速 圈/7.5s，中心喉管高度h为2m，a为旋转溜槽倾角，λ为消减系数。；α(°)为旋转溜槽倾角； L0 (m)为溜槽有效长度；ω(rad/s)为溜槽旋转角速度；μ为溜槽对炉料的摩擦系数。高炉布料相关情况见表1。

2.1.2  圆形布料溜布矿模型计算

圆形布料溜槽布矿模型计算公式及相关参数：

Vk1= 

Vk2= （Vk1* Vk1+0.5*g*h）1/2

VK3=λ* Vk2*cosa

VK4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=Vk4*sina

Vy=Vk4*cosa

圆溜槽计算时最高点和最低点的炉料所围成区域组成炉料布料区域，5高炉目前使用圆溜槽半径0.97m，计算横截面积0.3695m2，由于炉料面积0.0629 m2，如炉料堆积过程中两端呈直角，则炉料堆积面积为0.0671 m2，与炉料横截面积较为接近，因此本模型取炉料两端为直角。通过角速度w和溜槽长度计算出最高点位于0.44m，最低点处于溜槽横截面中心，本次计算忽略溜槽本身厚度影响，计算如表1，通过MATLAB模拟计算51和50度角时最远位置布料、最近位置和料宽见表2。

2.1.3  圆形布料溜槽布焦模型计算

圆形布料溜布焦模型计算公式及相关参数：

VJ1= 

VJ2= （VJ1* Vk1+0.5*g*h）1/2

VJ3=λ* VJ2*cosa

VJ4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=VJ4*sina

Vy=VJ4*cosa

通过MATLAB模拟计算51和50度角时最远位置布料、最近位置和料宽见表3。

2.2  方形溜槽布料情况

方形布料溜槽示意图及相关受力分析见图2。

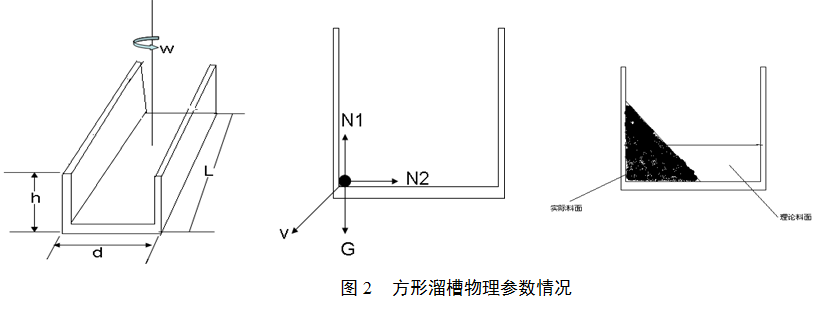
2.2.1  方形溜槽布料数值设定

设定料线为H，Q为炉料流量kg/s，S为料流开口面积m2，ρ为密度kg/m3，高炉布料溜槽转速 圈/7.5s，中心喉管高度h为2m，a为旋转溜槽倾角，λ为消减系数。；α(°)为旋转溜槽倾角；L0 (m)为溜槽有效长度；ω(rad/s)为溜槽旋转角速度；μ为溜槽对炉料的摩擦系数。

2.2.2  方形布料溜布矿模型计算

方形布料溜布焦模型计算公式及相关参数：

Vk1= 

Vk2= （Vk1* Vk1+0.5*g*h）1/2

VK3=λ* Vk2*cosa

VK4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=Vk4*sina

Vy=Vk4*cosa

方溜槽计算时最高点和最低点的炉料所围成区域组成炉料布料区域，5高炉目前备用方溜槽长3m，内壁宽0.97m，外壁宽1.2m，高0.67m，其中下部壁厚0.14m， 计算横截面积0.35141m2，由于炉料面积0.0629 m2，与炉料横截面积较为接近，因此本模型取炉料两端为直角。计算出最高点位于0.35m，最低点处于溜槽横截面中心，通过MATLAB模拟计算51和50度角时最远位置布料、最近位置和料宽见表4。

2.2.3  方形布料溜布焦模型计算

方形布料溜布焦模型计算公式及相关参数

VJ1= 

VJ2= （VJ1* VJ1+0.5*g*h）1/2

VJ3=λ* VJ2*cosa

VJ4= (2*g*(cosα-μ*sinα)*L0+4*π2*ω2*sinα*(sinα+μ*cosα) *L02+v32)1/2

Vx=VJ4*sina

Vy=VJ4*cosa

通过MATLAB模拟计算51和50度角时最远位置布料、最近位置和料宽见表5。

3  不同布料溜槽模型计算结果对比

3.1布矿情模型计算结果对比

圆形溜槽布矿模型模拟轨迹如图3，方形溜槽布矿模型模拟轨迹如图4。

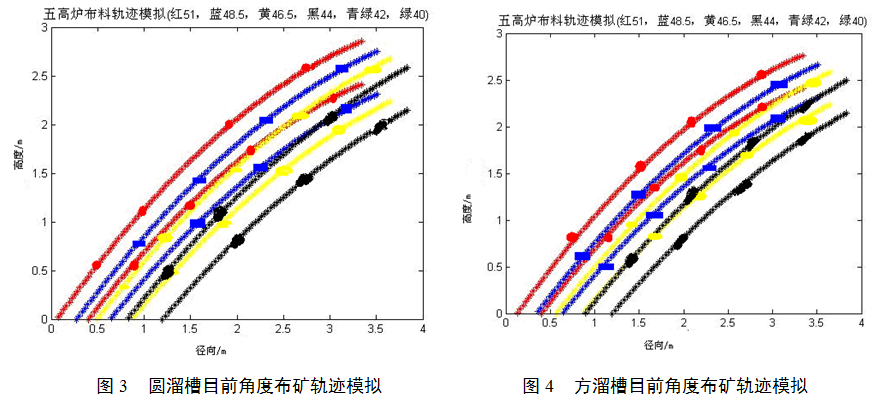
从图3和图4看51度角调度最外炉料落点圆形溜槽较方形溜槽靠近炉墙，布料角度相差1度圆溜槽炉料分布相差小1.2mm，随着布料角度的缩小，两种溜槽的布料宽度都有所增加，结果如下：

（1）圆溜槽布料角度相差1度炉料分布相差76mm，方溜槽布料角度相差1度炉料分布相差77.2mm；

（2）圆溜槽最远点较方溜槽最远点远69mm；

（3）圆溜槽随布料角度递减过程中布料带宽有所增加，1度角增加约11mm；

（4）方溜槽随布料角度递减过程中布料带宽有所增加，1度角增加约9.8mm；

3.2  布焦情模型计算结果对比

圆形溜槽布焦模型模拟轨迹如图5，方形溜槽布焦模型模拟轨迹如图6；

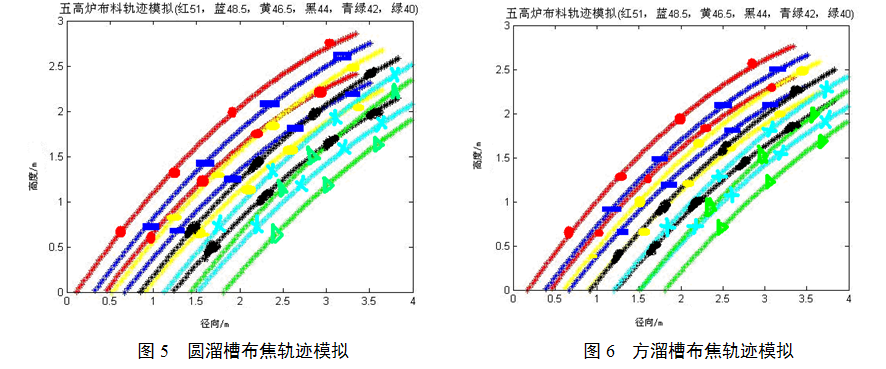
从图5和图6看51度角调度最外炉料落点圆形溜槽较方形溜槽靠近炉墙，布料角度相差1度圆溜槽炉料分布相差小1.8mm，随着布料角度的缩小，两种溜槽的布料宽度都有所增加，结果如下：

（1）圆溜槽布料角度相差1度炉料分布相差72.6mm，方溜槽布料角度相差1度炉料分布相差74.4mm，

（2）圆溜槽最远点较方溜槽最远点远67mm；

（3）圆溜槽随布料角度递减过程中布料带宽有所增加，1度角增加约9.4mm；

（4）方溜槽随布料角度递减过程中布料带宽有所增加，1度角增加约7.6mm；

4  结语

（1）圆形溜槽布料同样角度炉料落点较方形溜槽距炉墙更近；布焦炭圆溜槽最远点较方溜槽最远点远67mm；布矿圆溜槽最远点较方溜槽最远点远69mm

（2）圆形溜槽布料角度相差1度较方形溜槽布料宽度小，布焦角度相差1度相差小1.8mm，布矿角度相差1度相差小1.2mm；

（3）无论方形溜槽还是圆形溜槽，随着布料角度递减过程，炉料落点宽度都有所增加，圆形溜槽增加幅度更大，圆形溜槽布矿随1度角增加约11mm、布焦增加9.4mm，方形溜槽布矿随1度角增加约9.8mm、布焦增加7.6mm；

5  参考文献

[1] 并罐式无钟炉顶布料蛇形偏料的研究[J]. 杜鹏宇，程树森，滕召杰.  北京科技大学学报. 2011(04)

[2] 无钟并罐式高炉周向不均匀布料的研究[J]. 任廷志.  钢铁研究学报. 1999(03)